I have a ‘go-to’ list of quality and up-to-date sources of information that I continuously draw upon either as a reference, for training, detecting patterns and trends, or comparison and evaluation.
I have mapped the list to the data science process, and the skills and knowledge supporting it. I hope that it will save you time and help focus on relevant and key aspects using quality, vetted information.
The following graph provides an outline of the data science process and the skills and knowledge required to practice it.
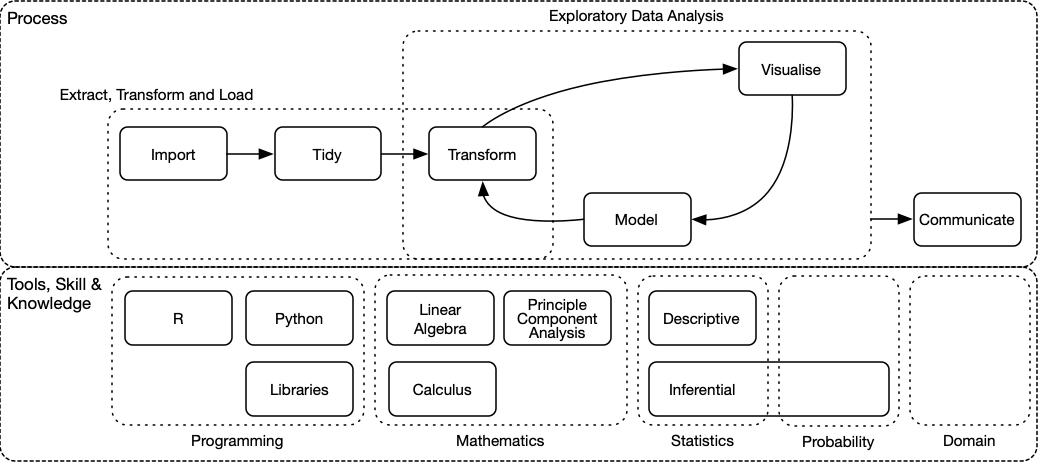
The data science process and tools, skills & knowledge that support it
The process section of the graph is an extract from R for Data Science by Hadley Wickham and Garrett Grolemund.
Summary of the data-science process
Data analysis is the process by which data becomes understanding, knowledge and insight. Hadley Wickham, July 2013
Extract, Transform & Load
The first, and probably the most labour intensive part of the data science process is to prepare and structure datasets to facilitate analysis, specifically importing, tidying and cleaning data. Hadley Wickham wrote about it in The Journal of Statistical Software, vol. 59, 2014.
Tidy Data
Tidying data1 aims to achieve the following:
- Each variable2 forms a column and contains values3
- Each observation4 forms a row.
- Each type of observational unit forms a table.
It attempts to deal with ‘messy data’, including the following issues:
- Column headers are values, not variable names.
- Multiple variables are stored in one column.
- Variables are stored in both rows and columns.
- Multiple types of observational units are stored in the same table.
- A single observational unit is stored in multiple tables.
Null Values/ Missing Data
Most models are typically unable to support data with missing values. The data science process will, therefore, include steps to detect and populate missing data.
It can occur anywhere between the importing and transforming stages. Models can be used to guess values for more complex treatments, whereas a simpler approach could use aggregation during transformation.
Transform
The result of the transform step in the data science process is to:
- reshape data, which could be used to produce tidy data,
- transform data, like rescaling5 of numeric values, or reducing dimensions of categorical values using Principle Component Analysis
- create new features, also known as ‘Feature Engineering’,
- or a combination of the above that typically results in aggregation.
Split, Apply, Combine
A common analytical pattern is to:
- split, group or nest data into pieces,
- apply some function to each piece,
- and to combine the results back together again.
It is also useful approach when modelling. Read more about it in Hadley Wickham’s paper: ‘The Split-Apply-Combine Strategy for Data Analysis’.
Visualisation & Modelling
In Feburary 2013 Hadley Wickham gave a talk where he described the interaction between visualisation and modelling very well.
Visualization can surprise you, but it doesn’t scale well. Modeling scales well, but it can’t surprise you.
Visualization can show you something in your data that you didn’t expect. But some things are hard to see, and visualization is a slow, human process.
Modeling might tell you something slightly unexpected, but your choice of model restricts what you’re going to find once you’ve fit it.
So you iterate. Visualization suggests a model, and then you use your model to factor out some feature of the data. Then you visualize again.
Table of resources in relation to Data Science
Process
Programming
Visualisation
| Area | Language | Source | # | Title | Author |
|---|---|---|---|---|---|
| Reference | Python | Web | 1 | matplotlib | Various |
| R | 2 | ggplot2 | Hadley Wickham, Various | ||
| Training | Python | 3 | Kaggle Learn: Data Visualisation | Aleksey Bilogur | |
| R | Book | 4 | ggplot2: Elegant Graphics for Data Analysis (Use R!) 2nd Edition | Hadley Wickham, Carson Sievert | |
| Web | 5 | Introduction to Data Science with R How to Manipulate, Visualize, and Model Data with the R Language | Garrett Grolemund |
Model
| Area | Language | Source | # | Title | Author |
|---|---|---|---|---|---|
| Reference | Python | Web | 1 | scikit-learn | Various |
| Training | 2 | Introduction to machine learning in Python with scikit-learn (video series) | Kevin Markham | ||
| 3 | Kaggle Learn: Machine Learning | Dan Becker | |||
| 4 | Kaggle Learn: Deep Learning | Dan Becker | |||
| 5 | Machine Learning Crash Course with TensorFlow APIs | ||||
| 6 | Machine Learning with Text in Python | Kevin Markham | |||
| Python, R | Web, Book | 7 | Machine Learning Mastery | Jason Brownlee | |
| R | Book | 8 | An Introduction to Statistical Learning with Applications in R | Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani | |
| 9 | Machine Learning with R - Second Edition: Expert techniques for predictive modeling to solve all your data analysis problems | Brett Lantz | |||
| Web | 10 | Statistical Learning | Trevor Hastie, Robert Tibshirani | ||
| 11 | Applied Predictive Modeling | Max Kuhn, Kjell Johnson | |||
| Training, Reference | Book | 12 | Applied Predictive Modeling | Max Kuhn, Kjell Johnson |
Statistics
Probability
| Area | Language | Source | # | Title | Author |
|---|---|---|---|---|---|
| Training | Mathematics | Web | 1 | Statistics 101 | Brandon Foltz |
| 2 | Statistics Foundations 1 | Eddie Davila | |||
| 3 | Statistics Foundations 2 | Eddie Davila | |||
| 4 | Statistics Foundations 3 | Eddie Davila |
Statistics
| Area | Language | Source | # | Title | Author |
|---|---|---|---|---|---|
| Reference | R | Web | 1 | Summary and Analysis of Extension Program Evaluation in R | Salvatore S. Mangiafico |
| Training | Mathematics | 2 | Statistics 101 | Brandon Foltz | |
| 3 | Statistics Foundations 1 | Eddie Davila | |||
| 4 | Statistics Foundations 2 | Eddie Davila | |||
| 5 | Statistics Foundations 3 | Eddie Davila | |||
| Python, R | Web, Book | 6 | Machine Learning Mastery | Jason Brownlee | |
| R | Book | 7 | An Introduction to Statistical Learning with Applications in R | Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani | |
| Web | 8 | Statistical Learning | Trevor Hastie, Robert Tibshirani |
Mathematics
Linear Algebra
| Area | Language | Source | # | Title | Author |
|---|---|---|---|---|---|
| Training | Mathematics | Book | 1 | Linear Algebra: Step by Step | Kuldeep Singh |
| Web | 2 | Mathematics for Machine Learning: Linear Algebra | David Dye, Samuel J. Cooper, A. Freddie Page | ||
| 3 | Essence of Linear Algebra | Grant Sanderson |
Calculus
| Area | Language | Source | # | Title | Author |
|---|---|---|---|---|---|
| Training | Mathematics | Web | 1 | Mathematics for Machine Learning: Multivariate Calculus | David Dye, Samuel J. Cooper, A. Freddie Page |
| 2 | Essence of Calculus | Grant Sanderson |
PCA
| Area | Language | Source | # | Title | Author |
|---|---|---|---|---|---|
| Training | Mathematics | Web | 1 | Mathematics for Machine Learning: PCA | Marc P. Deisenroth |
Described in R for Data Science: Exploratory Data Analysis↩
A variable is a quantity, quality, or property that you can measure. Height, weight, sex, etc.↩
A value is the state of a variable when you measure it. The value of a variable may change from measurement to measurement. 152 cm, 80 kg, female, etc.↩
An observation, or data point, is a set of measurements made under similar conditions (you usually make all of the measurements in an observation at the same time and on the same object). An observation will contain several values, each associated with a different variable. Each person.↩
Standardisation, Normalisation & Box-Cox transformations for example↩